Now that Aaron Hertzmann’s pointed it out, I’m noticing all the time that my perception of a scene doesn’t much match what a camera captures. Starts out lightweight; by the end he delves into some current research.
For good or ill, reading the ancient Wavefront OBJ model format (now 32 years old) is still a thing. Aras Pranckevičius compares the speeds of various popular OBJ readers (and an earlier one on optimizing such code). The readers vary considerably: a range of 70x in speed! He admits it’s a fair bit apples vs. oranges – each reader has different goals and two are multithreaded – but it’s worth a look if you read in such models. He also put all the test code in a repo for testing. Fun for me to see that the Minecraft Rungholt model created with my Mineways software gets used as a benchmark.
Large models? Try the coronavirus. The article’s just some visualizations presented in the NY Times, in the billion atoms range (sorry, not interactive, and your browser may appear to lock up – be patient).
Make meshes smaller and faster? I need to find some time someday to poke at meshoptimizer, an open-source project I’ve heard good things about and that has a lot of features.
AI-generated imagery has been rapidly evolving. If you missed DALL-E 2, here’s a pleasant, long video about it (or see their short marketing video) – worth the time. Midjourney is a related effort from another group with an emphasis on styles; you can sign up for the beta (but your GPU time is limited, so spend it wisely, perhaps building on others’ work). Video about both, with a bit more explanation. But wait, there’s more! So very much more. Among those many links I found this midjourney artist’s style dump is worth a skim.
I’m thinking I should always make the sixth element in these lists something goofy. This time it’s Coca-Cola Byte (two cans for just $14.77, plus $6.95 min. shipping).
This new illusion is fantastic – I did a screen cap of it (below) just to make sure they weren’t cheating with a GIF. That said, you might not see it – 14% of people don’t. And, for me, it’s much stronger on my PC than my phone. The authors note that the larger the better; here’s their big one.
The Moana scene now has a USD version. Other companies are offering up USD scenes, such as Animal Logic and Intel (with Sponza variants in USD and other formats). See item #18 for other model collections of all sorts.
Well, that’s maybe not the most tantalizing title, but it’s about right (and I did mis-title it originally – see the URL).
[And, before I start: to give a virtual space or two a try next week, register for I3D 2022 – happening next week, May 3-5, 2022 – for free. Due to COVID, they continue to experiment with ways to connect attendees through various means. Virtually see you there – say “hi” if you see me.]
I had a chat with Patrick Cozzi on the podcast “Building the Open Metaverse.” Our episode came out on Tuesday. It was fun, I rambled on about various topics. But after it was over I thought of other things I had neglected to mention or clarify, plus pointers to resources, plus… So, I thought I’d add a few tidbits here, with links as possible.
The negative themes I’ve been seeing lately in some articles about “the metaverse” are along these lines:
The metaverse is a long time off from being fully realized,
I agree with all of these to some large extent! Short of direct brain interfacing, having a full-featured “you feel like you’re there, you can walk around and touch things” holodeck-like experience looks way unlikely. “The metaverse” is definitely peaking on the hype cycle, even though Gartner says it’s further than 8 years out (which is as far out as they ever go). The Economist says cell phone sales are declining, so investors are looking for, hoping for, the Next Big Thing. So, yes, lots of hype and people floating technologies, 90% of which will fail. That’s nothing new, happens with all new tech.
The “who’d want to go there?” question is the more interesting one, on a few levels. Do we truly want to visit Chipotle in the metaverse? Is Powerpoint more compelling? Going to see a concert “live” via VR could be fun once or twice for the novelty and simplicity, but ultimately seems a bit of a hollow experience. If we value a live experience, say seeing a play vs. watching a film, we like to get all four dimensions aligned, close as possible in XYZ real space and time. Shift any of those, even if it’s “well, that famous person was in the room next door giving a speech and we all saw them on a giant TV screen outside” and there’s a loss of immediacy (and loss of bragging rights). Or even this, which I’ve certainly experienced.
At “holodeck-level” support, you could indeed have all sorts of experiences become available. Sail the seven seas as a pirate with others (oh, wait, there’s already Sea of Thieves), see if you can survive a zombie apocalypse (OMG where do I start?), or just chill out alone under the ocean (ABZÛ). I don’t think we want lots more realism, e.g., I truly don’t want to feel a bullet hit me or what falling off a skyscraper is really like, a la “the artwork formerly known as PainStation” (and if you do want that, go get this and don’t let me know how it works out).
Which gets to the last point, of the metaverse already being here. I admit to entirely losing myself in Valheim for hours when playing with my two (grown, each living elsewhere) sons. Making “actual” persistent changes with people you know in a virtual world, one where there’s no real save and restore system, is compelling – 10 million people agree with me (and the game is still not officially released).
Minecraft is the ultimate example of how making changes is great. It’s the best-selling game of all time. For a long time there was no actual game goal, beyond “survive the creepers” and other monsters. Even with that, it’s still not much of an adventure, more just virtual Legos. But what Legos they are! I think a major part of its success was an accident, that it was written in Java, which could be easily decompiled – Minecraft has over 100,000 mods for it.
Just being social is fine, too. I remember around 2005 wanting to quit the grind of playing the original World of Warcraft (“monster’ll be back in 15 minutes – see you then”). I had been tapering off, mostly been playing the auction house for a month at the end, making a pile of gold coins as sort of a mini-game. I ended my time there by going around newbie zones and holding informal trivia quizzes (“what’s the name of Harry Potter’s owl?”) and sending winners money. It was about the most fun I had in the game, interacting with strangers, since I didn’t have a group of people I played with. Other people liked the quizzes, too. I remember one stranger responding to the reward I sent, messaging me back about how they had been feeling down when they joined that night, but simply winning a little unexpected prize with their real-world knowledge had lifted their spirits.
All that said, I hardly think “the metaverse is here, game over.” There’s lots we can work on that helps immersion, interconnectivity, and much else. I talk about these a bit in the podcast, such as good data interchange through USD, glTF, or whatever other means evolve. Having objects developers or users could purchase and use in various shared spaces is intriguing (though for games I believe mostly unrealistic, beyond costuming – bringing a stirruped horse, let alone a spaceship, to a game about ancient Rome is going to break the balance). Buying a virtual item easily usable as content, vs. having artists and programmers spend days or weeks making a bespoke version for a single use in a game or film, seems like a huge efficiency and variety win. We’ve seen this “sell a hat” model work (and crash) in single games. This should be doable with a rich enough simulation representation.
That’s another area where I think one element of the metaverse is “here” (wherever “here” is). The idea of digital twins of the world, where you can test and train without fear of serious consequences, is being used to design factories, train robots and autonomous vehicles, and for other industrial uses. BIM, building information modeling, has been around a good long while, and covers similar ground as a digital twin – a virtual model of the building you can use for maintenance or upgrading operations after it’s built. There’s of course tons of other simulations out there – from viruses to stellar evolution – but the ones I like are when the virtual and real overlap, Pokemon Go–style or otherwise.
My sense of the metaverse is of technologies – hardware and software – that extend our senses. Do I need the fully realized 100 meter wide and ridiculously-long Street from Snow Crash? I liked that book, but that place sounds kinda dull and limited. Do I need to have all my senses overridden by the virtual? Doing so opens up a lot of questions, most involving some episode of Black Mirror…
I see extending our senses as more open and organic, where the real world and the virtual connect in diverse and fascinating ways. Ignore the obvious “almost all the world’s knowledge at our fingertips.” We meet with distant friends to play in a virtual space. We scan a QR code in a museum’s room to learn about the art on the walls. We hold up our phone to instantly translate a sign in a foreign language. Our car hits a pothole and registers the jolt (through a cell phone app or from the car itself) with the city; enough jolts from the community and a crew is sent out to fill the hole in. All of these are “obvious” now, but thirty years ago they were barely conceivable. And these, plus those we don’t yet even dream of, will become obvious and seamless in the future.
Now to take a walk outside. It’s a bit cold, but the sun’s out and I need some bananas. The world’s a convincing simulation.
(And hyperlinks are yet another lovely example of new technology quietly layering atop the old, making for a richer world. The unseen just behind the seen. Imagine a world where you can’t use links. If you want to reference something, you write “go to the library and look up this article in The New Yorker from two months ago, if your library has it available.” Welcome to 1990. I’m amazed we got anything done back then.)
[Feel like commenting? I’m interested, but comments on this blog are dicey – we’ve had too much spam. Easier is to respond in the tweet. – Eric]
I discovered this podcast, Building the Open Metaverse, through a tweet from Morgan McGuire. As chief scientist at Roblox, he has some interesting things to day.
Another podcast about videogame creation is Our Machinery. Episode 9 sounded interesting, interviewing the creator of Teardown, which is a pretty amazing voxel-based simulation game engine. I only just started this podcast, and the first seven minutes were mostly just chit-chat; looks like it gets more technical after that.
While we’re in videogame mode, I liked this album of models from Assassin’s Creed: Unity, particularly this and this (but they’re all quite nice).
Want a full-featured, battle-tested, physically based camera model? Give Nick Porcino’s a look. He kindly pointed it out to me due to my Twitter poll on “film back”, which has some interesting comments.
The New York Times has a number of Github projects, including a US COVID data set. A friend made a short movie of it (spoiler: it doesn’t end well, so far). There are tricky data visualization questions he’s grappling with (and hasn’t landed on answers yet), e.g., if a large area, low population county gets just a case or two, it lights up like it’s a major outbreak. Which remind me: I recommend the book The Data Detective (which sounded dull to me, but was not – Tim Harford is great at telling tales). And that, in turn, reminds me of Humble Pi, which I gave to a lot of people for Christmas – a great bathroom book. The author, Matt Parker, has a ton of YouTube videos, if that’s your preference.
I love the crabs, I admit it (and if you’re a crab lover, check out these robot crabs). The plastic teddy bear driving the horseshoe crab is my favorite:
I asked about this topic on Twitter, whether backface culling is a mesh or material property in your favorite renderer. The comments are great. Poll’s open until Monday – please do join in, if you like.
An entertaining rant in the Communications of the ACM (of all things) about why you shouldn’t ever look at patents.
If you want to use paint brushes on your iPad, make a Light Strokes system. If you don’t, the demo reels are fun to watch.
This article surprised me, about ten image formats the world allegedly forgot. Checking my own system right now (using the wonderful, free Everything finder on Windows), I see hundreds of BMPs loaded this year used in various applications, including UE4, Visual Studio, Maya, and 3DS MAX; TGA gets extensive use in Minecraft PBR resource packs; VRML is mostly dead but is still commonly used in the 3D print field. Some I agree with: TIFF is happily almost gone, good riddance (some traces in Houdini, Maya, and others – still seen for some terrain files on the USGS site, though (update: Angelo Pesce says it’s used in Photoshop still and sometimes is preferred over PSD. The horror, the horror.)); PCX is essentially defunct (the wonderful G3D uses it extensively and that’s it); AFAIK Maya and no one else uses IFF (and Irfanview can’t open them anyway).
Orano’s site is quite impressive graphically, running in the browser. I don’t particularly care about or even know what this company does (nuclear mumble something?), but I like that they splashed out for cool interlinked graphical tidbits. Try the “Live the Experiences” menu in the upper right, and scroll down to the bottom of each page for an interactive demo.
Townscaper is lovely, and a basic version is now free in the browser. Two minutes of semi-random clicking gave me this:
Mineways is my little hobby project. It exports models from Minecraft, for making animations or for 3D printing. It’s just turned 10 years old, and has been downloaded over a million times, from what I can gather (about 300 downloads a day currently). So, I thought I’d summarize some of the lessons I’ve learned from developing this interactive app.
Useful error messages: The most boring part of any interactive application, but vital. Recently I received the error message “An Error Occurred Installing iOS 15 on iPhone.” This is a prime example of “not useful.” Googling around and wading through the “buy our software to fix this” come-ons, I found the problem was maybe that there wasn’t enough memory free on my phone. Indeed, one Google Photos purge later, that was it.
Instead of sending your users on a possibly fruitless search expedition, or them just giving up on your software, spell out what’s going wrong.
I’ve noticed a tendency to have extremely terse error messages, installation instructions, and explanations in general. It’s as if every word costs us a dollar (hmmm, I guess it could, with localization…), so it’s like we play a game of making the messages as short as possible. Or we’re embarrassed to fully explain the solution, “everyone should already know that; I’ll feel I’ll look dumb and will insult my users if I write it all out.” You aren’t dumb, and no you won’t.
Over time, the error messages in Mineways have gotten longer and longer, as new problems get reported by users. Really, I should change a few to optionally take the user to a web page describing what to do.
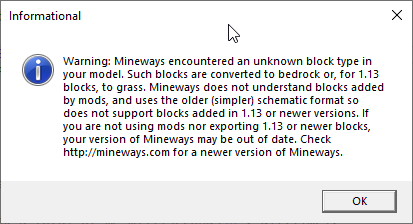
As a user, I’m happy to get as much information as I can. Please give it to me, I won’t mind. I could stop this post right here, as I’d say that’s the main thing I’ve learned.
Eat your own dogfood: I’m lucky in that I actually want to use Mineways, that’s why I originally wrote it. Using your own software makes you realize things that could be better. This can unfortunately sometimes lead to feeping creaturism, as more and more crazy options get added, to the point where the author is the only one who understands how to use their program. If you can leave the basics in place and make the frills and power-user features available but not distracting, great.
One example for Mineways is basic scripting. Every UI action has some simple, English script command for it. Nothing clever, very little to learn, no Python or even loop constructs in the scripting. But for power users, if you want to do a bunch of exports in a row, e.g., tiles of terrain, it’s invaluable. Or if you can put a script on the command line if you want to start Mineways up with certain export options or viewing a particular world. This system doesn’t get in the way of most people simply using the program as-is. I made scripting in good part for myself, so that I could restart where I left off, and also do at least some minimal QA testing before making a new release. But I quickly realized it could help users in many other ways.
Professionals: consider paying someone to use your software for some real activity, not just unit testing, and have them report bugs and annoyances. If it’s a graphics app, bonus: you get a cool demo/video/stills out of it.
Eat others’ dogfood: And pay attention to what you’re eating. It took me a mere 9.5 years to realize I should add drag and drop to Mineways. Drop a level.dat file, Mineways figures out you’re opening a Minecraft world. Drop a terrain*.png file, you’re assigning a resource pack. Drop a saved OBJ, VRML, or USD file, you’re wanting to restore all the export setting you used to make that model file. Drop a script, run the script.
I realized I should add this simple feature (40 lines of sloppy coding – maybe an hour of work learning how to add the event and respond to it) only after doing some recent testing on Cinema 4D. That package’s UI is just wonderful in some areas. Blender is by far the most popular “consumer” of Mineways’ output (both are free, and amateurs – in the best sense of the word – are the main users), but has poor flow in this area. I was blinded by Blender’s involved model import system: File | Import | select file type, paste directory into the dialog, choose model file. Cinema 4D just loads whatever you drop on its viewport, as best it can (perhaps popping up a dialog as needed). I now use this drag and drop feature in Mineways all the time.
Another example: In trying “the competition,” Jmc2Obj, I found I should export to OBJ model files the “map_d” alpha texture for the material. I had not done so for many years, because support in other applications was spotty, sometimes worse if map_d was included (and, to be honest, because long ago I found Jmc2Obj literally unusable, I couldn’t get an export out of it to save my soul; it’s now a lot better). I had also convinced myself that “hey, there’s an alpha channel in the four-channel PNG file itself, that should simply be enough – it should get used.” Some applications indeed use this alpha channel without fuss, but others (looking at you, Blender) do not. Seeing that Jmc2Obj exported map_d, and testing a bunch of modern model-viewing applications, convinced me to do the same (I actually had to finally build and patch G3D, a model viewer I otherwise love and recommend for Mineways preview, as setting “map_d” to an RGBA PNG file in unpatched G3D would use the red channel instead of the alpha).
Keep in contact: I have a Google Group and Minecraft Forum thread for announcements, Github for issues, a subreddit and Discord server for questions, betas, and other stuff – users can take their pick. I also reveal my email address (gasp! (it’s erich@acm.org)) on the Mineways site’s contact page. 15 years ago it was perhaps unwise to expose your email address anywhere, as you’d be asking to be a spam magnet (I still did so and lived to tell the tale). Nowadays Gmail’s filter and other services have become great at weeding out the junk. I was a bit leery of adding a Discord server, but I’m thrilled to find that a few other users have enjoyed helping out, answering common questions.
So, hobbyists, stop hiding as SpaceTurtle258 and not giving users any way to reach you. Pros, can your users easily ask for help? Can they find the locations of the support, forum, live chat, email, and whatever other services you offer? This information should be linked in some form from every web page on your site. Same thing for you, blog writer or webmaster – people should be able to contact you. If you don’t want to hear from users, start to question your life choices.
That’s it (especially the installation instructions and error messages!). Mineways’ code is nothing brilliant. Could be a lot better, but it’s free, and a hobby. I try to make it work reasonably well and be user friendly. It does one small task – model export – and does it in a fairly reasonable fashion. Happily, it’s also been extremely useful in my paid work for testing out and learning about the new USD scene format, for example.
I like finishing posts with a little eye candy. So, here, lava refracting through some water (from some recent test images):
JG-RTX resource pack, USD output, path-traced in Omniverse Create – all free
I had some “well, they’re sorta graphics-related” links left from making yesterday’s blog post. Here you go:
MeshOptimizer – definitely graphical, a software system that encompasses a wide range of optimization techniques for real-time display of meshes. Listed today because I mentioned another resource by the same author (on Vulkan) yesterday – I didn’t want to overload that post with “all-things-zeux.”
Desmos Global Math Art Content results – kids use weird equations to make line art creations on a graphing calculator app. Click on one and open up the folders to see the crazy. Future ShaderToy programmers in training, I guess…
Reading the first chapter of Ray Tracing Gems II (free to download, and also now re-available in soft and hardcover through Apress, soon through Amazon I assume), I found I’ve been misusing “depth of field” for these many decades. That’s of course a teaser for you to check it out yourself. I like the author’s tone of exasperation. That said, “defocus blur” seems unlikely to fully catch on.
Electronic Arts has taken a patent pledge to not sue anyone reusing their accessibility-centered technology patents. Not a lot of patents covered, but a nice thing nonetheless.
This announcement reminded me of a 1993 article, Patent Nonsense, by John Walker, one of the founders of Autodesk. He talks about the idea of companies making cross-licensing pools of patents.
Which reminded me of another article that he wrote worth a read, “Creation/Evolution,” about how trying to get a design perfect at the start is a fool’s errand. Which reminds me of the book Adapt, by Tim Harford, which I just started and am enjoying… OK, I’ll stop the flow of consciousness here.
The Microsoft Teams virtual backgrounds page is a bit of a surprise, even after noting it’s under the “Educator Center” heading. My new favorite Teams background:
